Сумма углов - это фундаментальное понятие в геометрии, которое имеет различные значения для разных типов фигур. Рассмотрим основные правила вычисления суммы углов в различных геометрических объектах.
Содержание
Сумма углов - это фундаментальное понятие в геометрии, которое имеет различные значения для разных типов фигур. Рассмотрим основные правила вычисления суммы углов в различных геометрических объектах.
Сумма углов в плоских фигурах
| Фигура | Формула суммы углов | Пример |
| Треугольник | 180° | Равносторонний: 60°+60°+60°=180° |
| Четырехугольник | 360° | Квадрат: 90°×4=360° |
| n-угольник | (n-2)×180° | Пятиугольник: (5-2)×180°=540° |
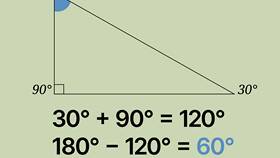
Доказательство для треугольника
Сумма углов треугольника всегда равна 180°. Это можно доказать следующим образом:
- Проведем прямую, параллельную одной из сторон треугольника
- Образовавшиеся углы при параллельной прямой будут равны углам треугольника
- Сумма углов на прямой составляет 180°
- Следовательно, сумма углов треугольника также равна 180°
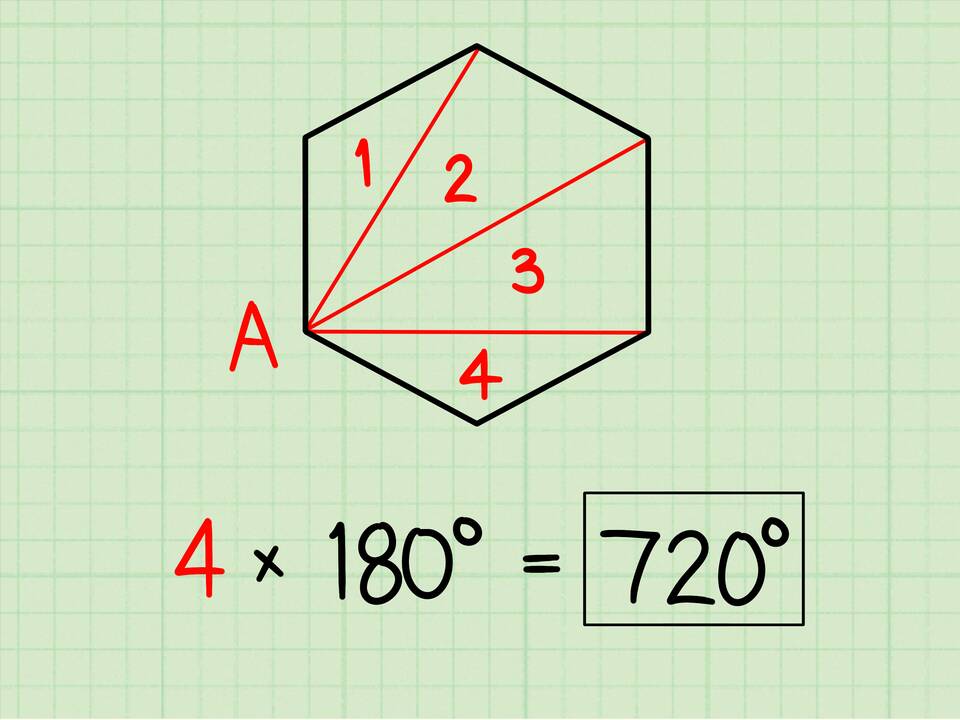
Сумма углов в многоугольниках
Формула для выпуклого n-угольника:
S = (n - 2) × 180°
где n - количество сторон (углов) многоугольника
Примеры расчета:
- Шестиугольник: (6-2)×180° = 720°
- Восьмиугольник: (8-2)×180° = 1080°
- Десятиугольник: (10-2)×180° = 1440°
Сумма внешних углов
Для любого выпуклого многоугольника сумма внешних углов, взятых по одному при каждой вершине, всегда равна 360°.
| Фигура | Сумма внешних углов |
| Треугольник | 360° |
| Четырехугольник | 360° |
| n-угольник | 360° |
Особые случаи
Для правильных многоугольников:
- Каждый внутренний угол = (n-2)×180°/n
- Каждый внешний угол = 360°/n
Пример для правильного пятиугольника:
- Сумма углов: (5-2)×180° = 540°
- Каждый угол: 540°/5 = 108°
- Внешний угол: 360°/5 = 72°
Заключение
Знание правил о сумме углов различных фигур является важным базисом для изучения геометрии. Эти принципы применяются при решении задач, доказательстве теорем и в практических расчетах. Запомнив основные формулы, вы сможете легко вычислять суммы углов для любых многоугольников.
